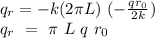Question

Drive an expression for heat transferred by a finite extended rod of uniform cross-section area with perfect insulated free end .

Answer 1

Step-by-step explanation:

hiiiii

Answer 2

Assumptions:

• Unidimensional heat transfer.

• Conduction coefficient is constant.

• 
  `T_(\infty) < T_(s).`

Step-by-step explanation:

Use the appropriated heat transfer equation (cylindrical coordinates),

`\frac {1}{r} \frac {d}{dr} (\ r \frac {dT}{dr}) + \frac {q}{k} \ = \ 0`

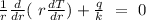
After separating variables and integrating we obtained the following expression,

`r(dT)/(dr) \ = \ - (q)/(2k) \ r^(2) \ + \ C_(1)`

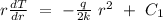
After repeating the procedure state above we obtained the following expression,

`T(r) \ = \ - (q)/(2k) \ r^(2) \ + \ C_(1) ln(r) \ + \ C_(2)`

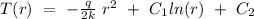
According to the image attached, the corresponding boundary values for the system are

`\left \{ {{(dT)/(dr)=0 \ , \ r={0}} \atop {T(r_(0))=T_(s)}} \right.`

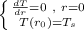
Then, the temperature distribution in the rod along r axis corresponds to,

`T(r) \ = \ (qr_(0)^(2))/(4k) (1 \ - (r^2)/(r_(0)^(2)) ) \ + \ T_(s)`

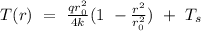
After deriving the function, we obtained the expression that follows,

`(dT)/(dr) \ = \ - (qr)/(2k)`

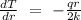
Evaluating the previous expression at the surface of the rod,

`(dT)/(dr) \lvert_{r = r_(0)}} \ = (- (qr_(0))/(2k))`

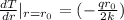
Answer:

The heat transferred by the finite extended rod corresponds to,

`q_(r) = -k(2 \pi L) (dT)/(dr)`

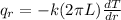
Replacing the derivate term, we obtained the expression that follows,

`q_(r)  = -k(2 \pi L) \ (- (qr_(0))/(2k))\\q_(r) \ = \ \pi \ L \ {q \ r_(0)`