Question

(a) Each person has two parents, four grandparents, eight great-grandparents, and so on. By summing a geometric sequence, find the total number of ancestors a person has going back (1) five generations, (2) 10 generations. normal growth pattern for children aged 3-11 follows an arithmetic sequence. Given a child measures 98.2 cm at age 3, and 109.8 cm at age 5, what is the common difference of the arithmetic sequence? What would the child's height at age 8 be?

Answer 1

The person has62 ancestors going back five generations.

The person has 2046 ancestors going back ten generations.

---------------------

The child's height at age 8 would be 127.2 cm.

Explanation:

The first sequence is a geometric sequence.

In a geometric sequence, each term is found by multiplying the previous term by a constant r.

We write a geometric sequence like this:

`{a, ar, ar^(2), ar^(3),...}`

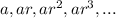
Where a is the first term and r is the commom factor.

The sum of the first n elements of a geometric sequence is:

`S = (a(1 - r^(n)))/(1-r)`

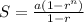
So, for the first exercise, our geometric sequence is:

{2,4,8,...},

so a = 2 and r = 2.

1)Find the total number of ancestors a person has going back five generations

S when n = 5, so:

`S = (a(1 - r^(n)))/(1-r) = (2*(1-2^(5)))/(1-2) = 62`

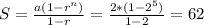
The person has 62 ancestors going back five generations.

2) Going back 10 generations:

S when n = 10, so:

`S = (a(1 - r^(n)))/(1-r) = (2*(1-2^(10)))/(1-2) = 2046`

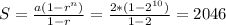
The person has 2046 ancestors going back ten generations.

-------------

The following question is related to an arithmetic sequence:

An arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant.

If the first term of an arithmetic sequence is a1 and the common difference is d, then the nth term of the sequence is given by:

`a_(n) = a_(1) + (n-1)d`.

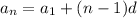We have the following sequence

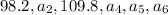`98.2, a_(2), 109.8, a_(4), a_(5), a_(6)`, in which
`a_(6)` is the child's height at age 8.

We have that:

`d = (109.8 - 98.2)/(2) = 5.8`

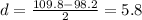
So

`a_(6) = a_(1) + 5d = 98.2 + 5*5.8 = 127.2`.

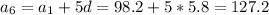The child's height at age 8 would be 127.2 cm.