Answer :
The standard Gibbs free energy is, -27640.414 J
The standard cell potential is, 0.29 V
Explanation :
First we have to calculate the
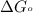 .
.
Formula used :
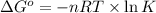
where,
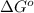 = standard Gibbs free energy = ?
= standard Gibbs free energy = ?
R = gas constant = 8.314 J/K.mole
n = number of moles = 1 mole
T = temperature =
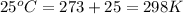
k = equilibrium constant =

Now put all the given values in this formula, we get:
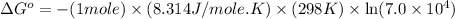
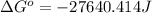
The standard Gibbs free energy is, -27640.414 J
Now we have to calculate the standard cell potential.
Formula used :
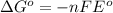
where,
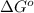 = Gibbs free energy = -27640.414 J
= Gibbs free energy = -27640.414 J
n = number of electrons = 1
F = Faraday constant = 96500 C/mole
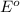 = standard e.m.f of cell = ?
= standard e.m.f of cell = ?
Now put all the given values in this formula, we get the Gibbs free energy.
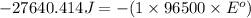
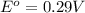
The standard cell potential is, 0.29 V