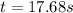Question

a ball is projected upward at time t = 0.00 s from a point on a roof 70 m above the ground. The ball rises, then falls and strikes the ground. The initial velocity of the ball is 82 m/s if air resistance is negligible. The time when the ball strikes the ground is closest to _____

Answer 1

Answer: 17.68 s

Step-by-step explanation:

This problem is a good example of Vertical motion, where the main equation for this situation is:

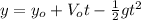`y=y_(o)+V_(o)t-(1)/(2)gt^(2)` (1)

Where:

`y=0` is the height of the ball when it hits the ground

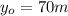`y_(o)=70 m` is the initial height of the ball

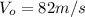`V_(o)=82m/s` is the initial velocity of the ball

`t` is the time when the ball strikes the ground

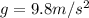`g=9.8m/s^(2)` is the acceleration due to gravity

Having this clear, let's find
`t` from (1):

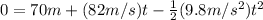`0=70m+(82m/s)t-(1)/(2)(9.8m/s^(2))t^(2)` (2)

Rewritting (2):

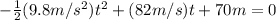`-(1)/(2)(9.8m/s^(2))t^(2)+(82m/s)t+70m=0` (3)

This is a quadratic equation (also called equation of the second degree) of the form
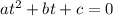`at^(2)+bt+c=0`, which can be solved with the following formula:

`t=\frac{-b \pm \sqrt{b^(2)-4ac}}{2a}` (4)

Where:

`a=-(1)/(2)(9.8m/s^(2)`

`b=82m/s`

`c=70m`

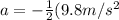
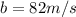
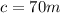
Substituting the known values:

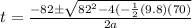`t=\frac{-82 \pm \sqrt{82^(2)-4(-(1)/(2)(9.8)(70)}}{2a}` (5)

Solving (5) we find the positive result is:

`t=17.68 s`