Question

Calculate the intensity of thermal radiation from a blackbody by using Raleigh-Jeans Law at a temperature of 1000 K and with a wavelength of 1000 nm (infrared), 500 nm (visible), and 100 nm (ultraviolet). (3 points) (b) Recalculate the above intensities using Plank's Law

Answer 1

Step-by-step explanation:

Given that,

Temperature = 1000 K

We need to calculate the intensity of thermal radiation from a black body

For wavelength 1000 nm

Using Raleigh-Jeans Law

`B_(k)=(8\pi kT)/(\lambda^4)`

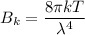
Put the value into the formula

`B_(k)=(8*\pi*1.38*10^(-23)*1000)/((1000*10^(-9))^(4))`

`B_(k)=346831.828956`

`B_(k)=34.68*10^(4)\ W`

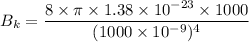
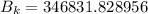
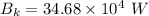
For wavelength 500 nm

`B_(k)=(8*\pi*1.38*10^(-23)*1000)/((500*10^(-9))^(4))`

`B_(k)=5549309`

`B_(k)=55.49*10^(5)\ W`

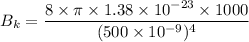
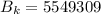
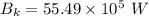
For wavelength 100 nm

`B_(k)=(8*\pi*1.38*10^(-23)*1000)/((100*10^(-9))^(4))`

`B_(k)=3.47*10^(9)\ W`

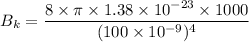
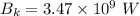
We need to calculate the intensity

Using Plank's Law

`E=(2hc^2)/(\lambda^5)*\frac{1}{e^{(hc)/(\lambda k T)}-1}`

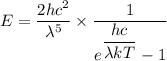
For wavelength 1000 nm

Put the value into the formula

`E=(2*6.63*10^(-34)*(3*10^(8))^2)/((1000*10^(-9))^5)*\frac{1}{e^{(6.63*10^(-34)*3*10^(8))/(1000*10^(-9)* 1.38*10^(-23)*1000)}-1}`

`E=65.65*10^(6)\ W/m^2.K^4`

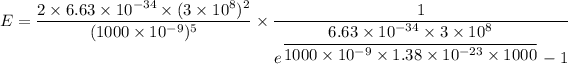
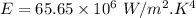
For wavelength 500 nm

`E=(2*6.63*10^(-34)*(3*10^(8))^2)/((500*10^(-9))^5)*\frac{1}{e^{(6.63*10^(-34)*3*10^(8))/(500*10^(-9)* 1.38*10^(-23)*1000)}-1}`

`E=11.56*10^(2)\ W/m^2.K^4`

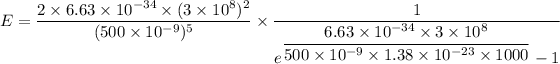
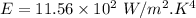
For wavelength 100 nm

`E=(2*6.63*10^(-34)*(3*10^(8))^2)/((100*10^(-9))^5)*\frac{1}{e^{(6.63*10^(-34)*3*10^(8))/(100*10^(-9)* 1.38*10^(-23)*1000)}-1}`

`E=3.032*10^(-44)\ W/m^2.K^4`

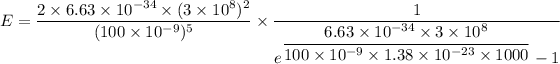
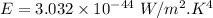
Hence, This is the required solution.