Step-by-step explanation:
Given that,
Temperature = 1000 K
We need to calculate the intensity of thermal radiation from a black body
For wavelength 1000 nm
Using Raleigh-Jeans Law
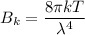
Put the value into the formula
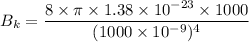
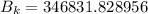
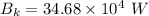
For wavelength 500 nm
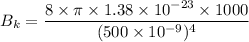
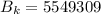
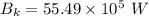
For wavelength 100 nm
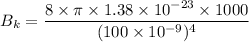
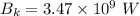
We need to calculate the intensity
Using Plank's Law
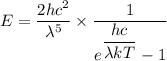
For wavelength 1000 nm
Put the value into the formula
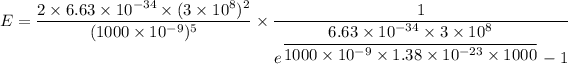
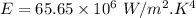
For wavelength 500 nm
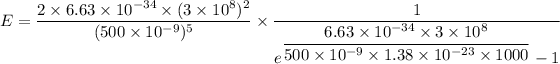
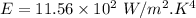
For wavelength 100 nm
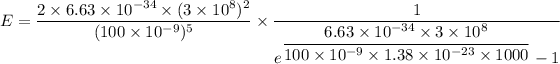
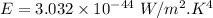
Hence, This is the required solution.