Question

Find at least the first four nonzero terms in a power series expansion about co = 0 for the general solution to the given differential equation y"+y=0. Page 2

Answer 1

Explanation:

Given is a differential equation

`y`

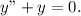
SInce it is a power series solution let us assume

`y =[tex]}`[/tex]

Find I and II derivative

`y=a_0+a_1x+...+a_nx^n+...`

`y'=a_1+2a_2x+3a_3x^2+....na_n x^n +...\\y`

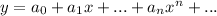
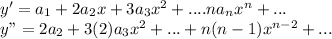
Now substitute in the given DE

2a_2 +3(2)a_3x^2+...+a_n n(n-1)x^{n-2} +... a_0+a_1x+....+a_nx^n +....=0\\\\a_{n-2} +n(n-1) a_n =0\\a_n = \frac{-a_{n-2}}{n(n-1)

Thus the solution is a power series with recurring formula

a_n = \frac{-a_{n-2}}{n(n-1)