Answer:
Reading is close to (b) 13.44 which is the best estimate of the period
Associated error,
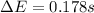
Given:
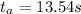
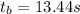
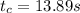
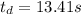
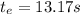
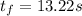
Solution:
1.The best estimate of the period can be calculated by the mean of the measurements and the one closest to the mean is the best estimate of the measurement:
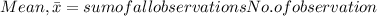
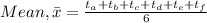
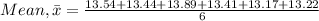
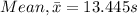
It is close to 13.44 s
2. Associated error is given by:
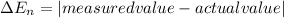
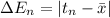
where
n = a, b,......, e
Now,
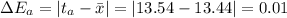
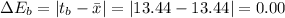
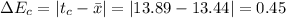
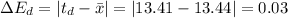
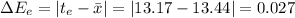
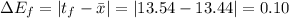
Mean Absolute Error,
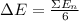
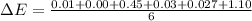
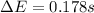
3. The assumption behind the estimation is population is considered to distributed normally.