Question

A student uses a stopwatch to measure the period of the pendulum of the Beverly clock in the corridor. His measurements are: (a) 13.54is (b) 13.44 s (c) 13.89 s (d) 13.41 s (e) 13.17s (f) 13.22 s . Calculate his best estimate of the period Calculate the associated error .Explain the assumptions behind your estimation of the error

Answer 1

Reading is close to (b) 13.44 which is the best estimate of the period

Associated error,
`\Delta E =0.178 s`

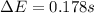
Given:

`t_(a) = 13.54 s`

`t_(b) = 13.44 s`

`t_(c) = 13.89 s`

`t_(d) = 13.41 s`

`t_(e) = 13.17 s`

`t_(f) = 13.22 s`

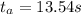
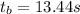
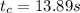
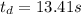
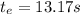
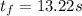
Solution:

1.The best estimate of the period can be calculated by the mean of the measurements and the one closest to the mean is the best estimate of the measurement:

`Mean, \bar {x} = \fra{sum of all observations}{No. of observation}`

`Mean, \bar {x} = (t_(a) + t_(b) + t_(c) +t_(d) + t_(e) + t_(f))/(6)`

`Mean, \bar {x} = (13.54 + 13.44 + 13.89 + 13.41 + 13.17 + 13.22)/(6)`

`Mean, \bar {x} = 13.445 s`

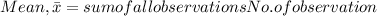
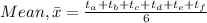
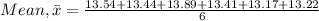
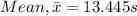
It is close to 13.44 s

2. Associated error is given by:

`\Delta E_(n) = |measured value - actual value|`

`\Delta E_(n) = |t_(n) - \bar {x}|`

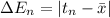
where

n = a, b,......, e

Now,

`\Delta E_(a) = |t_(a) - \bar {x}| = |13.54 - 13.44| = 0.01`

`\Delta E_(b) = |t_(b) - \bar {x}| = |13.44 - 13.44| = 0.00`

`\Delta E_(c) = |t_(c) - \bar {x}| = |13.89 - 13.44| = 0.45`

`\Delta E_(d) = |t_(d) - \bar {x}| = |13.41 - 13.44| = 0.03`

`\Delta E_(e) = |t_(e) - \bar {x}| = |13.17 - 13.44| = 0.027`

`\Delta E_(f) = |t_(f) - \bar {x}| = |13.54 - 13.44| = 0.10`

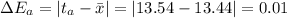
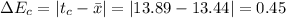
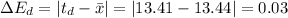
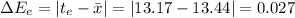
Mean Absolute Error,
`\Delta E = (\Sigma E_(n))/(6)`

`\Delta E = (0.01 + 0.00 + 0.45 + 0.03 +0.027 + 1.10)/(6)`

`\Delta E =0.178 s`

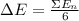
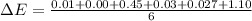
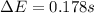
3. The assumption behind the estimation is population is considered to distributed normally.