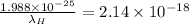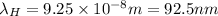Answer:

Given:
n = 9
n' = 1
Solution:
In Bohr's Model, the radiation emitted by a hydrogen atom on transition from the energy level, n = 9 to n' = 1 is given by:
![\Delta E_(H) = 13.6[(1)/(n^(2)) - (1)/(n'^(2))]](https://img.qammunity.org/2020/formulas/physics/college/5utagbbv4put8hzz63hfjuwt07vpjht6fs.png) (1)
(1)
Also,

where
h= Planck's constant
c = speed of light
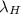 = wavelength of radiation emitted by hydrogen atom
= wavelength of radiation emitted by hydrogen atom
Therefore, eqn (1) becomes:
![(hc)/(\lambda_(H)) = 13.6[(1)/(n^(2)) - (1)/(n'^(2))]](https://img.qammunity.org/2020/formulas/physics/college/65t3dxleyks2yaxtxjnsvx5vqde69f6h20.png)
![(6.626* 10^(- 34)* 3* 10^(8))/(\lambda_(H)) = 13.6[(1)/(9^(2)) - (1)/(1^(2))]](https://img.qammunity.org/2020/formulas/physics/college/vsz30xpd7hwt2u89yq8cya83i8ha2rt6vl.png)
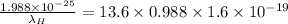
(since, 1 eV =
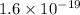 )
)