Answer:
-6 + 6√10 and -6 - 6√10
Explanation:
By the distance formula,
The distance between the points
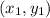 and
and
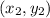 is,
is,
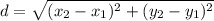
So, the distance between (-6,-6) and (x,-5) is,
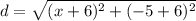
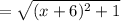
According to the question,
d = 19 units,
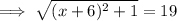
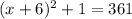
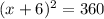
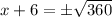
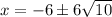
Hence, the possible values of x would be,
-6 + 6√10 and -6 - 6√10