Question

Calculate the pressure drop along 1 m length ( horizontal ) of a smooth 25 mm diameter pipe when water flows through it at 735 l/hr. What is the average shear stress on the pipe wall ?

Answer 1

average shear stress is 0.0673 N/m²

Step-by-step explanation:

given data

length L = 1 m

diameter d = 25 mm = 0.025

flow Q = 735 l/hr = 2.04167 ×
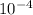`10^(-4)` m³/s

to find out

average shear stress

solution

we know here dynamic viscosity μ at room temperature 20 degree is = 1001 ×
`10^(-6)` Pa-s

so here V average is express as

V average = Q/A

here A is area = πd²/4 = π(0.025)²/4

V average = Q/A

V average = 2.04167 ×
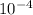`10^(-4)` / ( π(0.025)²/4 )

V avg = 0.415923

so

Reynolds number = ρ×V×d / μ ...............1

put here value

Reynolds number = 1000×0.415923×0.025 / 1001 ×
`10^(-6)`

Reynolds number = 10387.68

that is greater than 2100

so it is turbulent flow

and friction factor f is

f = 0.3164 /
`Re^(0.25)`

f = 0.03134

so here

pressure drop = f ×L×ρ×V² / 2d ...................2

pressure drop = 1000 ×0.03134×1×(0.415923)² / 2(0.025)

pressure drop = 108.2 N/m²

and

average shear stress = ρ × v²

here v = Vavg × √(F/8) = 0.415 √(0.03134/8) = 0.0259

so

average shear stress = 1000 × (0.0259)²

average shear stress is 0.0673 N/m²