Question

A circular section of 25 mm diameter is welded (all the way around) to a wall and subject to a torsional load. Calculate the unit second moment of area for the circular weld pattern. 3 (Enter the value in mm without any decimal places)

Answer 1

`38330mm^(4)`

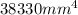
Step-by-step explanation:

As we know that the moment of area of polar is also known as the second moment of area. It is used to describe resistance to torsional deformation, on cylindrical objects with an invariant cross section area.

Therefore, mathematically second moment of area can be written as,

`A= (\pi R^(4) )/(2)`

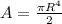
Here, R is the radius of circular cross section.

Given that a circular section is welded to a wall has a diameter,

`D=25mm`

Therefore,

`R=(D)/(2) \\R=(25)/(2) mm`

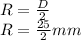
Therefore, second moment of area for the circular weld pattern is,

`A= (\pi ((25)/(2)) ^(4) )/(2)\\A=38330mm^(4)`