Question

Given the system of equations, match the following items.

2 x - y = 0 x + y = -3

A. [0 -1

-3 1]

B. [2 0

1 -3]

C. [2 -1

1 1]


x determint
y determint
system determent

Answer 1

A. x-determinant

B. y-determinant

C. system determinant

Explanation:

The "augmented" matrix for the system is the system coefficient matrix with the constants added as an extra column on the right:

`\left[\begin{array}c2&-1&0\\1&1&-3\end{array}\right]`

The x-determinant is the determinant of the system matrix after the x-coefficients have been replaced by the constants:

`\left|\begin{array}{cc}0&-1\\-3&1\end{array}\right|`

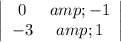
The y-determinant is the determinant of the system matrix after the y-coefficients have been replaced by the constants:

`\left|\begin{array}{cc}2&0\\1&-3\end{array}\right|`

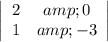
Of course, the system determinant is the determinant of the matrix of coefficients of the variables:

`\left|\begin{array}{cc}2&-1\\1&1\end{array}\right|`

_____

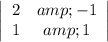
Comment on these determinants

Cramer's rule tells you the solution to the system is ...

x = (x-determinant)/(system determinant)

y = (y-determinant)/(system determinant)