Question

In a double-slit experiment, the third-order maximum for light of wavelength 520 nm is located 17 mm from the central bright spot on a screen 1.6 m from the slits. Light of wavelength 630 nm is then projected through the same slits. How far from the central bright spot will the second-order maximum of this light be located?

Answer 1

The distance from the central bright spot is 13.73 mm.

Step-by-step explanation:

Given that,

Wavelength = 520 nm

Width d= 17 mm

Distance L= 1.6 m

Order = 3

We need to calculate the distance from the central bright spot

Using formula of distance

`y=(m\lambda L)/(d)`

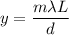
Put the value into the formula

`y=(3*520*10^(-9)*1.6)/(17*10^(-3))`

`y=0.0001468=146.8*10^(-6)\ m`

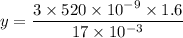
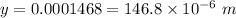
Now, the wavelength is changed to 630 nm

We need to calculate the distance from the central bright spot with the second order of this light

`y=(2*630*10^(-9)*1.6)/(146.8*10^(-6))`

`y=0.0137=13.73*10^(-3)\ m`

`y=13.73\ mm`

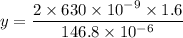
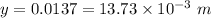
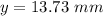
Hence, The distance from the central bright spot is 13.73 mm.