Answer:
The final image relative to the diverging lens at 9.0 cm.
Step-by-step explanation:
Given that,
Focal length of diverging lens = -6.18 cm
Focal length of converging lens = 12.5 cm
Distance of object = 36.9 cm
We need to calculate the image distance of converging lens
Using formula of lens
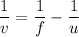
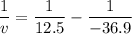

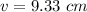
We need to calculate the image distance of diverging lens
Now, object distance is
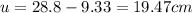
Using formula of lens
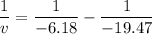
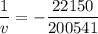
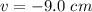
The image is formed 9.0 cm to the left of the diverging lens.
Hence, The final image relative to the diverging lens at 9.0 cm.