Question

Show explicitly that ▽ . B-0 near a long straight wire carrying a current I. HINT: you may use Cartesian coordinates, but another choice might make it easier

Answer 1

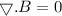`\bigtriangledown.B=0` is proved.

Step-by-step explanation:

The magnetic field in the long current carrying wire is,

`B=(\mu_(0)I )/(2\pi r ) \phi`

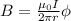
Here, I is the current, B is the magnetic field.

Now, by using cylindrical coordinates for the divergence of B.

`\bigtriangledown.B=(1)/(s) (d)/(d\phi) B`

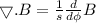
Put the value of B in above equation.

`\bigtriangledown.B=(1)/(s) (d)/(d\phi)((\mu_(0)I )/(2\pi r ) \phi)\\\bigtriangledown.B=0`

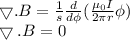
Hence, it is prove that for a long current I carrying wire magnetic field divergence that is
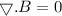`\bigtriangledown.B=0`.