Show explicitly that ▽ . B-0 near a long straight wire carrying a current I. HINT: you may use Cartesian coordinates, but another choice might make it easier

Question

asked Jan 7, 2020 90.7k views

1 Answer

Yam Tal · Answer 1 · 2020-01-11T10:48:48+0000

Answer:

$\bigtriangledown.B=0$ is proved.

Step-by-step explanation:

The magnetic field in the long current carrying wire is,

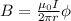
$B=(\mu_(0)I )/(2\pi r ) \phi$

Here, I is the current, B is the magnetic field.

Now, by using cylindrical coordinates for the divergence of B.

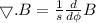
$\bigtriangledown.B=(1)/(s) (d)/(d\phi) B$

Put the value of B in above equation.

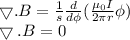
$\bigtriangledown.B=(1)/(s) (d)/(d\phi)((\mu_(0)I )/(2\pi r ) \phi)\\\bigtriangledown.B=0$

Hence, it is prove that for a long current I carrying wire magnetic field divergence that is
$\bigtriangledown.B=0$ .