Question

Copper has a density of 8.94 g/cm3 . If a factory has an ingot of copper with a mass of 125 pounds and the ingot is drawn into a wire with a diameter of 9.50 mm, how many feet of wire can be produced? (454 grams = 1 pound)

Answer 1

Answer: The length of copper wire is 295.68 feet.

Step-by-step explanation:

To calculate volume of a substance, we use the equation:

`\text{Density of substance}=\frac{\text{Mass of substance}}{\text{Volume of substance}}`

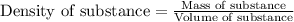
Density of copper =
`8.94g/cm^3`

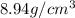
Mass of copper = 125 pounds = 56750 g (Conversion factor: 1 pound = 454 g)

Putting values in above equation, we get:

`8.94g/cm^3=\frac{56750g}{\text{Volume of copper}}\\\\\text{Volume of copper}=6347.87cm^3`

The volume of copper wire is
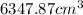`6347.87cm^3`. The copper wire is in the shape of cylinder.

The equation used to calculate the volume of cylinder is:

`V=\pi r^2h`

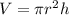
where,

V = volume of copper wire =
`6347.87cm^3`

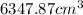
r = radius of the copper wire =
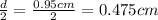`(d)/(2)=(0.95cm)/(2)=0.475cm` (Conversion factor: 1 cm = 10 mm)

h = length/ height of the copper wire = ?

Putting values in above equation, we get:

`6347.87cm^3=(3.14)* (0.475)^2* h\\\\h=8960cm`

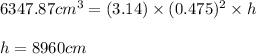
Converting this value of length of copper wire into feet, we use the conversion factor:

1 cm = 0.033 foot

So,
`8960cm=0.033* 8960=295.68ft`

Hence, the length of copper wire is 295.68 feet.