Answer:
Maximum area = 9 sq units
Explanation:
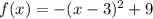
which represents the area . As it is a quadratic equation it represents the parabola . And the vertex of the parabola will maximum area of for some value of x
let f(x) = y
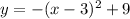
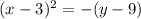
Comparing it with the standard equation of parabola

we get h=3 and y=9
where (h,k) is the vertex (3,9)
Hence the maximum area of the rectangle will be 9