Answer:
(D) 2.55 eV is absorbed
Step-by-step explanation:
For an electron located in an inner orbit to jump an upper orbit, it needs an energy equal to the difference between the two quantized orbits. This energy comes from the absorption of a photon with the same energy required. The formula for the energy levels of a Hydrogen atom is:
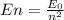
where
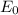 is the energy of the ground state and n is the energy level or state. Finding
is the energy of the ground state and n is the energy level or state. Finding
 and
and
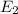 :
:
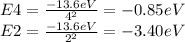
Finally we find the energy difference between n=4 and n=2 state:
