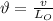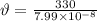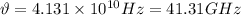Answer:
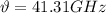
Given:
Pressure,
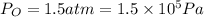
Temperature, T =
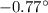 = 273 + (- 0.77) = 272.23 K
= 273 + (- 0.77) = 272.23 K
Diameter of oxygen molecule,
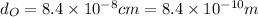
Speed of sound, v = 330 m/s
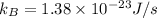
Solution:
Mean free path of oxygen is given by:
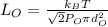
Now, substituting the given values in the above formula:
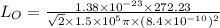
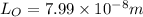
Now, the frequency,
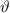 is given by:
is given by:
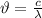
Since, mean free path = wavelength =
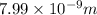
Therefore,