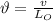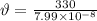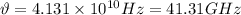Question

At what frequency would the wavelength of sound in air be equal to the mean free path of oxygen molecules at 1.5 atm pressure and -0.77°C? Take the diameter of an oxygen molecule to be 8.4 x 10^-8 cm and the speed of sound to be 330 m/s.

Answer 1

`\vartheta = 41.31 GHz`

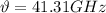
Given:

Pressure,
`P_(O) = 1.5 atm = 1.5* 10^(5) Pa`

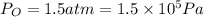
Temperature, T =
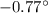`- 0.77^(\circ)` = 273 + (- 0.77) = 272.23 K

Diameter of oxygen molecule,
`d_(O) = 8.4* 10^(- 8) cm = 8.4* 10^(-10) m`

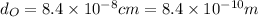
Speed of sound, v = 330 m/s

`k_(B) = 1.38* 10^(- 23) J/s`

Solution:

Mean free path of oxygen is given by:

`L_(O) = (k_(B)T)/(√(2)P_(O)\pi d_(O)^(2))`

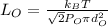
Now, substituting the given values in the above formula:

`L_(O) = (1.38* 10^(- 23)* 272.23)/(√(2)* 1.5* 10^(5)\pi* (8.4* 10^(- 10))^(2))`

`L_(O) = 7.99* 10^(-8) m`

Now, the frequency,
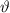`\vartheta` is given by:

`\vartheta = (c)/(\lambda)`

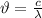
Since, mean free path = wavelength =
`7.99* 10^(-9) m`

Therefore,

`\vartheta = (v)/(L_(O))`

`\vartheta = (330)/(7.99* 10^(-8))`

`\vartheta = 4.131* 10^(10) Hz = 41.31 GHz`