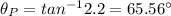Answer:
Polarizing angle,
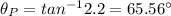
Given:
Critical angle,
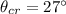
Solution:
Now, in Total Internal Reflection (TIR), the critical angle for cubic zirconia is given by:
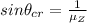 (1)
(1)
where
 = refractive index of zirconia
= refractive index of zirconia
From eqn (1):
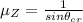
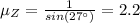
Now, the angle of polarization is given by:
tan
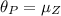
Therefore,