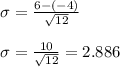Answer:
The standard deviation is calculated to be 2.886 in the given interval
Step-by-step explanation:
Uniform distribution in an interval [a,b] is defined by the function
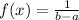
The variance of the distribution is given by
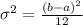
Hence the standard deviation is given by
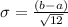
Applying values we get