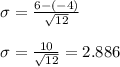Question

A random variable x is uniformly distributed over the interval (-4, 6). Find the standard deviation of x.

Answer 1

The standard deviation is calculated to be 2.886 in the given interval

Step-by-step explanation:

Uniform distribution in an interval [a,b] is defined by the function

`f(x)=(1)/(b-a)`

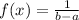
The variance of the distribution is given by

`\sigma ^(2)=((b-a)^(2))/(12)`

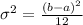
Hence the standard deviation is given by

`\sigma =((b-a))/(√(12))`

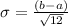
Applying values we get

`\sigma =(6-(-4))/(√(12))\\\\\sigma = (10)/(√(12))=2.886`