Answer:
E=-1.51 eV.
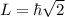
Step-by-step explanation:
The nth level energy of a hydrogen atom is defined by the formula,
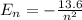
Given in the question, the hydrogen atom is in the 3p state.
Then energy of n=3 state is,
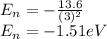
Therefore, energy of the hydrogen atom in the 3p state is -1.51 eV.
Now, the value of L can be calculated as,
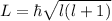
For 3p state, l=1
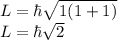
Therefore, the value of L of a hydrogen atom in 3p state is
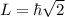 .
.