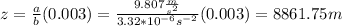Answer:
8861.75 m approximately 8862 m
Step-by-step explanation:
We need to remember Newton's 2nd Law which says that the force experienced by an object is proportional to his acceleration and that the constant of proportionality between those two vectors correspond to the mass of the object.
 for the weight of an object (which is a force) we have that the acceleration experienced by that object is equal to the gravitational acceleration, obtaining that
for the weight of an object (which is a force) we have that the acceleration experienced by that object is equal to the gravitational acceleration, obtaining that
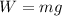
For simplicity we work with
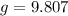
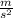 despiting the effect of the height above sea level. In this problem, we've been asked by the height above sea level that makes the weight of an object 0.30% more lighter.
despiting the effect of the height above sea level. In this problem, we've been asked by the height above sea level that makes the weight of an object 0.30% more lighter.
In accord with the formula
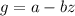 the "normal" or "standard" weight of an object is given by
the "normal" or "standard" weight of an object is given by
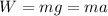 when
when
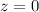 , so we need to find the value of
, so we need to find the value of
 that makes
that makes
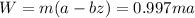 meaning that the original weight decrease by a 0.30%, so now we operate...
meaning that the original weight decrease by a 0.30%, so now we operate...
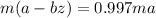 now we group like terms on the same sides
now we group like terms on the same sides
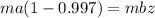 we cancel equal tems on both sides and obtain that
we cancel equal tems on both sides and obtain that