Question

How many solutions does the equation x1 + x2 + x3 = 100 have, where the xi are non-negative integers integers?

Answer 1

The equation:
`x_1+x_2+x_3=100` Where the xi are non-negative integers has 5050 solutions

Explanation:

We need to find a combination with repetitions to find how many solutions have the equation:

`x_1+x_2+x_3=100`

We know the xi are non-negative integers and we have three unknowns in the equation, so:

m= 3 (The number of unknowns in the equation)

r= 99 (result - 1)

The combination is:

`C(m+r-1,r)\\C(3+99-1,99)\\C(101,99)`

`C(101,99)=(101!)/(99!(101-99)!) \\C(101,99)=5050`

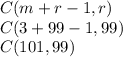
The number of solutions to this equation is: 5050 solutions