Question

Which number line represents the solution set for the inequality –4(x + 3) ≤ –2 – 2x?

A number line from negative 7 to 7 in increments of 1. A point is at negative 5 and a bold line starts at negative 5 and is pointing to the right.
A number line from negative 7 to 7 in increments of 1. A point is at 5 and a bold line starts at 5 and is pointing to the right.
A number line from negative 7 to 7 in increments of 1. A point is at 5 and a bold line starts at 5 and is pointing to the left.
A number line from negative 7 to 7 in increments of 1. A point is at negative 5 and a bold line starts at negative 5 and is pointing to the right.

Answer 1

I'm terrible at explaining so here's a screenshot

- Ripper

Explanation:

Answer 2

For this case we have the following inequality:

`-4 (x + 3) \leq-2-2x`

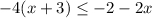
Applying distributive property on the left side we have:

`-4x-12 \leq-2-2x`

Adding 2x to both sides of the inequality we have:

`-4x + 2x-12 \leq-2\\-2x-12 \leq-2`

Adding 12 to both sides of the inequality we have:

`-2x \leq-2 + 12\\-2x \leq10`

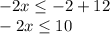
Dividing by 2 to both sides of the inequality:

`-x \leq \frac {10} {2}\\-x \leq5`

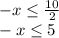
Multiplying by -1 on both sides, taking into account that the sense of inequality changes:

`x \geq-5`

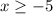
Thus, the solutions are given by all values ​​greater than or equal to -5.

ANswer:

See attached image

Option A