Answer:
a)The efficiency =40.78 % or nearly 41%.
Step-by-step explanation:
Given that
maximum temperature = 850 K
minimum temperature = 298 K
We know that condition for optimum pressure for maximum work out put is given as
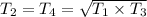
So
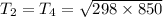

We also know that efficiency of Brayton cycle given
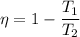
So now by putting the values
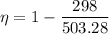
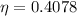
So the efficiency =40.78 % or nearly 41%.