Question

A hydrogen-filled balloon to be used in high altitude atmosphere studies will eventually be 100 ft in diameter. At 150,000 ft, the pressure is 0.14 lb/in2 and the temperature is - 67°F. Assume the balloon is spherical in shape. What is the diameter of the hydrogen balloon at the ground at 14.7 lb/in2 and 68°F

Answer 1

The answer is 11.7 ft

Step-by-step explanation:

You can use the combined gas law from Boyle's law, Charles's law, and Gay-Lussac's Law. Only because hydrogen behaves like an ideal gas for this conditions.

`(p_1 V_1)/(T_1) = (p_2 V_2)/(T_2)`

where the subscripts denote the pressure "p", volume "V" and the temperature "T" (in Kelvin) at two different times. Let's consider
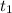`t_1` as the balloom at 150,000 ft so

`p_1 = 0.14 \ lb/in^2`

`V_1 = (4)/(3) \pi R_1^3 = 523598.77 \ ft^3`

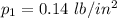
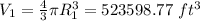
and
`T_1 = -67^\circ F = 218.15\ K`.

Then,
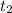`t_2` is the moment when the balloon is on the ground.

`p_2 = 14.7 \ lb/in^2` and
`T_2 = 68^\circ F = 293.15\ K`.

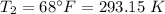From the first equation,

`V_2 = (p_1 V_1 T_2)/(T_1 p_2)`, then

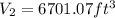`V_2 = 6701.07 ft^3` and the radius would be

`R_2 = \sqrt[3]{(3 V_2)/(4 \pi)} = 11.7 \ ft`.