Question

A population of kangaroos is growing at a rate of 2% per year, compounded continuously. If the growth rate continues, how many years will it take for the size of the population to reach 150% of its current size according to the exponential growth function? Round your answer up to the nearest whole number, and do not include units.

Answer 1

It will take 20 years for the size of the population to reach 150% of its current size according to the exponential growth function.

Step-by-step explanation:

The exponential growth function is given by:

`P(t) = P(0)e^(rt)`

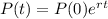
In which
`P(t)` is the population after t years,
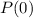`P(0)` is the initial population, e is the Euler number and r is the growth rate(decimal).

In this problem, we have that:

A population of kangaroos is growing at a rate of 2% per year, compounded continuously. This means that
`r = 0.02`.

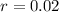If the growth rate continues, how many years will it take for the size of the population to reach 150% of its current size according to the exponential growth function?

This is the value of t when
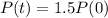`P(t) = 1.5P(0)`. So

`P(t) = P(0)e^(rt)`

`1.5P(0) = P(0)e^(0.02t)`

`e^(0.02t) = 1.5`

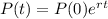
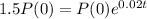
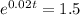
Since ln and e are inverse operation, we apply e to both sides of the equation to find t.

`\ln{e^(0.02t) }= ln(1.5)`

`0.02t = 0.4055`

`t = (0.4055)/(0.02)`

`t = 20.27`

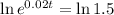
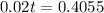
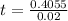
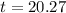
Rouding to the nearest whole number, it is 20 years.

It will take 20 years for the size of the population to reach 150% of its current size according to the exponential growth function.

Answer 2

The correct answer is 20 years.

Step-by-step explanation:

It is given that the growing rate is 2% or 2/100 = 0.02

This rate got increased to 150%

The formula for exponential growth is:

A = Pe^rt

Let the initial population be 100%

150 = 100.e^0.02*t

3/2 = e^0.02t

1.5 = e^0.02t

After taking log from both the sides:

ln(1.5) = 0.02t * ln(e) [ln(e) = 1]

ln(1.5) = 0.02t

t = ln(1.5)/0.02

t = 20.27

Thus, it will take around 20 years for the size of the population to reach 150 percent of its present size on the basis of the exponential growth function.