Question

The waiting times between a subway departure schedule and the arrival of a passenger are uniformly distributed between 0and 7minutes. Find the probability that a randomly selected passenger has a waiting time greater than3.25minutes.

Answer 1

.535714

Explanation:

(7-3.25)/7=.535714

Max time in uniform distribution minus the waiting time. divided the sum of this by the waiting time = answer

Answer 2

0.5357

Explanation:

The waiting times are uniformly distributed between 0 and 7 minutes. We need to find the probability that a randomly selected passenger has a waiting time greater than 3.25 minutes.

The formula to use for uniform distribution is:

`P( X > x) = (b-x)/(b-a)`

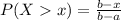
where,

b is the upper limit of the distribution which is 7 in this case.

a is the lower limit of the distribution which is 0 in this case.

x is the concerned value which is 3.25 in this case.

Using these values, we get:

`P( X > 3.5) = (7-3.5)/(7-0)=0.5357`

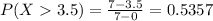
This means, the the probability that a randomly selected passenger has a waiting time greater than 3.25 minutes is 0.5357