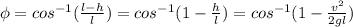Question

A mass of 4kg suspended by a light string 2m long and at rest is projected horizontally with a velocity of 1.5 m/s. find the angle made by the string when the mass comes to momentary rest

​

Answer 1

19.5°

Step-by-step explanation:

The energy of the mass must be conserved. The energy is given by:

1)
`E=(1)/(2)mv^2+mgh`

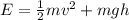
where m is the mass, v is the velocity and h is the hight of the mass.

Let the height at the lowest point of the be h=0, the energy of the mass will be:

2)
`E=(1)/(2)mv^2`

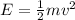
The energy when the mass comes to a stop will be:

3)
`E=mgh`

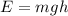
Setting equations 2 and 3 equal and solving for height h will give:

4)
`h=(v^2)/(2g)`

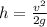
The angle ∅ of the string with the vertical with the mass at the highest point will be given by:

5)
`cos\phi=(l-h)/(l)`

where l is the lenght of the string.

Combining equations 4 and 5 and solving for ∅:

6)
`\phi={cos}^(-1)((l-h)/(l))={cos}^(-1)(1-(h)/(l))={cos}^(-1)(1-(v^2)/(2gl))`