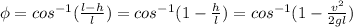Answer:
19.5°
Step-by-step explanation:
The energy of the mass must be conserved. The energy is given by:
1)
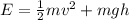
where m is the mass, v is the velocity and h is the hight of the mass.
Let the height at the lowest point of the be h=0, the energy of the mass will be:
2)
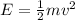
The energy when the mass comes to a stop will be:
3)
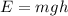
Setting equations 2 and 3 equal and solving for height h will give:
4)
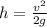
The angle ∅ of the string with the vertical with the mass at the highest point will be given by:
5)
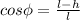
where l is the lenght of the string.
Combining equations 4 and 5 and solving for ∅:
6)