Answer:
C.Restricted domain :
 ,
,
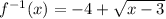
Explanation:
We are given that a function is not one - to-one.
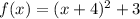
Suppose
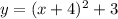
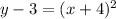
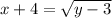
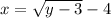
Hence,
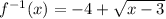
We know that domain of f(x) is converted into range of
 and range of f(x) is converted into domain of
and range of f(x) is converted into domain of
 .
.
Substitute x=3 then we get
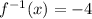
Domain of
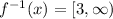
Range of
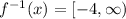
Domain of f(x)=
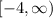
Restricted domain :

Hence, restricted domain of f(x) that makes the function one-to-one .