Answer:
Percentage of bromine-88 left after 35.0 s = 23%
Step-by-step explanation:
Radioactive decay follows first order kinetics.
Given:
Half life of Br-88 = 16.3 s
time = 35.0 s
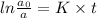
where,
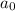 = Initial concentration of radioactive substance
= Initial concentration of radioactive substance
a = Amount left after time 't'
K = rate constant
Half-life = 0.693/K
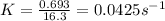
now, substitute the value of rate constant and t (35.0 s) in the formula,
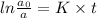
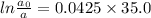
Let a0 (initial concentration of bromine-88) be 100.
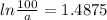
[a] = 22.6% = 23%
Percentage of bromine-88 left after 35.0 s = 23%