Answer:
The pressure reduces to 2.588 bars.
Step-by-step explanation:
According to Bernoulli's theorem for ideal flow we have
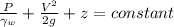
Since the losses are neglected thus applying this theorm between upper and lower porion we have
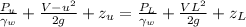
Now by continuity equation we have
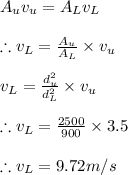
Applying the values in the Bernoulli's equation we get
