Answer:
The required vectors are
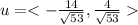 and
and
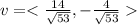 .
.
Explanation:
Given information: P(-4,-2) and Q(3,-4).
We need to find the two vectors parallel to
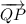 with length 2.
with length 2.
If
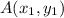 and
and
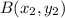 , then
, then
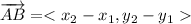
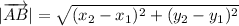
Using the above formula we get
vector QP is,
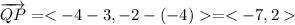
Magnitude of vertor QP is,
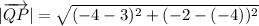
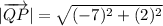
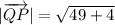
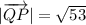
Using vector is
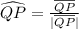
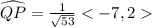
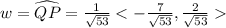
Multiply vector w by 2 to get a parallel vector parallel of QP in same direction.
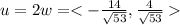
Multiply vector w by -2 to get a parallel vector parallel of QP in opposite direction.
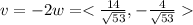
Therefore the required vectors are
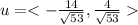 and
and
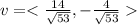 .
.