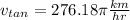Answer:
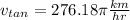
Explanation:
Givens:
Where
 is the radius and
is the radius and
 is the period, that is, the time used to complete one rotation.
is the period, that is, the time used to complete one rotation.
The tangential speed is defined as:
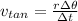
Where
 is the angular movement or the angle, and
is the angular movement or the angle, and
 the time used during the movement.
the time used during the movement.
In this case, the angular movement is one rotation which is
 . Now, we replace all given values:
. Now, we replace all given values:

Therefore, the tangential speed is