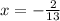For this case we must solve the following equation:
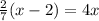
So:
We apply distributive property to the terms within parentheses:
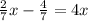
Add
 on both sides of the equation we have:
on both sides of the equation we have:
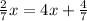
Subtracting 4x from both sides of the equation we have:

We multiply by 7 on both sides of the equation:
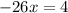
We divide by -26 on both sides of the equation:
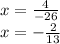
ANswer: