Question

Equilateral triangle ABC has an area of \sqrt{3}√ ​3 ​ ​​ . If the shaded region has an area of \piπK − \sqrt{3}√ ​3 ​ ​​ , what is the value of K?

Answer 1

The value of k = 4/3

Explanation:

* Lets explain how to solve the problem

- An equilateral triangle ABC is inscribed in a circle N

- The area of the triangle is √3

- The shaded area is the difference between the area of the circle

and the area of the equilateral triangle ABC

- The shaded are = k π - √3

- We need to find the value of k

* At first lets find the length of the side of the Δ ABC

∵ Δ ABC is an equilateral triangle

∴ Its area = √3/4 s² , where s is the length of its sides

∵ The area of the triangle = √3

∴ √3/4 s² = √3

- divide both sides by √3

∴ 1/4 s² = 1

- Multiply both sides by 4

∴ s² = 4 ⇒ take √ for both sides

∴ s = 2

∴ The length of the side of the equilateral triangle is 2

* Now lets find the radius of the circle

- In the triangle whose vertices are A , B and N the center of the circle

∵ AN and BN are radii

∴ AN = BN = r , where r is the radius of the circle

∵ The sides of the equilateral angles divides the circle into 3 equal

arcs in measure where each arc has measure 360°/3 = 120°

∵ The measure of the central angle in a circle equal the measure

of the its subtended arc arc

∵ ∠ANB is an central angle subtended by arc AB

∵ The measure of arc AB is 120°

∴ m∠ANB = 120°

- By using the cosine rule in Δ ANB

∵ AB = 2 , AN = BN = r , m∠ANB = 120°

∴
`(2)^(2)=r^(2)+r^(2)-2(r)(r)cos(120)`

∴
`4=r^(2)+r^(2)-2(r)(r)(-0.5)`

∴
`4=r^(2)+r^(2)-(-r^(2))`

∴
`4=r^(2)+r^(2)+r^(2)`

∴
`4=3r^(2)`

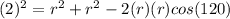
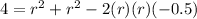
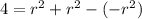
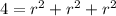
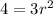
- Divide both sides by 3

∴
`r^(2)=(4)/(3)`

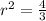
- Take square root for both sides

∴ r = 2/√3

* Lets find the value of k

∵ Area circle = πr²

∵ r = 2/√3

∴ Area circle = π(2/√3)² = (4/3)π

∵ Area shaded = area circle - area triangle

∵ Area triangle = √3

∴ Area shaded = (4/3) π - √3

∵ Area of the shaded part is π k - √3

- Equate the two expressions

∴ π k - √3 = (4/3) π - √3

∴ k = 4/3

* The value of k = 4/3