Question

A rectangle with a length of L and a width of W has a diagonal of 10 inches. Express the perimeter P of the rectangle as a function of L.

Answer 1

The expression which represents the perimeter P of the rectangle as a function of L is:

`Perimeter=2(L+√(100-L^2))`

Explanation:

The length and width of a rectangle are denoted by L and W respectively.

Also the diagonal of a rectangle is: 10 inches.

We know that the diagonal of a rectangle in terms of L and W are given by:

`10=√(L^2+W^2)`

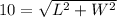
( Since, the diagonal of a rectangle act as a hypotenuse of the right angled triangle and we use the Pythagorean Theorem )

Hence, we have:

`10^2=L^2+W^2\\\\i.e.\\\\W^2=100-L^2\\\\W=\pm √(100-L^2)`

But we know that width can't be negative. It has to be greater than 0.

Hence, we have:

`W=√(100-L^2)`

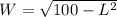
Now, we know that the Perimeter of a rectangle is given by:

`Perimeter=2(L+W)`

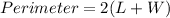
Here we have:

`Perimeter=2(L+√(100-L^2))`