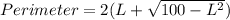Answer:
The expression which represents the perimeter P of the rectangle as a function of L is:
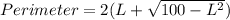
Explanation:
The length and width of a rectangle are denoted by L and W respectively.
Also the diagonal of a rectangle is: 10 inches.
We know that the diagonal of a rectangle in terms of L and W are given by:
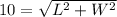
( Since, the diagonal of a rectangle act as a hypotenuse of the right angled triangle and we use the Pythagorean Theorem )
Hence, we have:
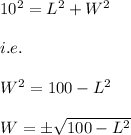
But we know that width can't be negative. It has to be greater than 0.
Hence, we have:
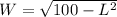
Now, we know that the Perimeter of a rectangle is given by:
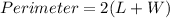
Here we have: