Question

To estimate the average students' scores in a standardize test, a sample of 35 scores yielded a mean of 80 and a standard deviation of 9. What is a lower limit for a 98% confidence interval for the population mean?

Answer 1

The lower limit for a 98% confidence interval for the population mean is 79.40.

Explanation:

Given : To estimate the average students' scores in a standardize test, a sample of 35 scores yielded a mean of 80 and a standard deviation of 9.

To find : What is a lower limit for a 98% confidence interval for the population mean?

Solution :

The confidence interval formula is given by,

`CI=\bar{x}\pm Z_c((\sigma)/(n))`

The lower limit is
`CI=\bar{x}-Z_c((\sigma)/(n))`

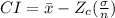
Where,
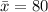`\bar{x}=80` is the mean

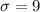`\sigma=9` is the standard deviation

n=35 is the number of element

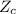`Z_c` at 98% is 2.33.

Substitute all values in the formula,

`CI=80-(2.33)((9)/(35))`

`CI=80-(2.33)(0.257)`

`CI=80-0.59881`

`CI=79.40`

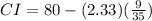
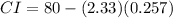
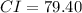
Therefore, The lower limit for a 98% confidence interval for the population mean is 79.40.