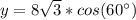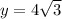Answer:
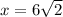
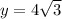
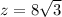
Explanation:
The cosine function is defined as:
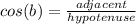
Where:
adjacent is the length of the side that contains angle b and angle 90 °
Hypotenuse is the length of the side opposite the angle of 90 °.
So if b is the angle of 45 ° we have that:
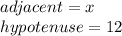
Thus:
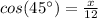
Now we solve the equation for x
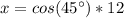
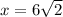
The sine function is defined as:
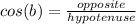
Where:
opposite is the length of the side opposite the angle of b
Hypotenuse is the length of the side opposite the angle of 90 °.
if b is the angle of 60 ° we have that:
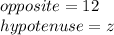
Thus:

Now we solve the equation for z
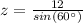
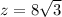
Finally we use the cosine function to find the value of y
if b is the angle of 60 ° we have that:
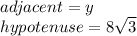
Thus:
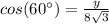
Now we solve the equation for y