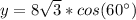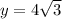Question

Find x, y and z.

( ANSWER NEEDS TO BE IN REDUCED RADICAL FORM )

Answer 1

`x =6√(2)`

`y=4√(3)`

`z =8√(3)`

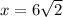
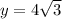
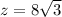
Explanation:

The cosine function is defined as:

`cos(b) = (adjacent)/(hypotenuse)`

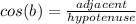
Where:

adjacent is the length of the side that contains angle b and angle 90 °

Hypotenuse is the length of the side opposite the angle of 90 °.

So if b is the angle of 45 ° we have that:

`adjacent = x\\hypotenuse = 12`

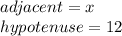
Thus:

`cos(45\°) = (x)/(12)`

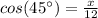
Now we solve the equation for x

`x = cos(45\°)*12`

`x =6√(2)`

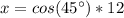
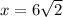
The sine function is defined as:

`cos(b) = (opposite)/(hypotenuse)`

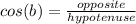
Where:

opposite is the length of the side opposite the angle of b

Hypotenuse is the length of the side opposite the angle of 90 °.

if b is the angle of 60 ° we have that:

`opposite = 12\\hypotenuse = z`

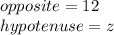
Thus:

`sin(60\°) = (12)/(z)`

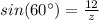
Now we solve the equation for z

`z = (12)/(sin(60\°))`

`z =8√(3)`

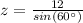
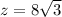
Finally we use the cosine function to find the value of y

if b is the angle of 60 ° we have that:

`adjacent = y\\hypotenuse = 8√(3)`

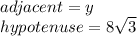
Thus:

`cos(60\°) = (y)/(8√(3))`

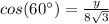
Now we solve the equation for y

`y = 8√(3)*cos(60\°)`

`y=4√(3)`

Answer 2

Part 1)
`x=6√(2)\ units`

Part 2)
`y=4√(3)\ units`

Part 3)
`z=8√(3)\ units`

Explanation:

In the right triangle of the right side

`cos(45\°)=(√(2))/(2)`

`cos(45\°)=(x)/(12)`

`(x)/(12)=(√(2))/(2)`

`x=6√(2)\ units`

In the right triangle of the left side

`tan(60\°)=(12)/(y)`

`tan(60\°)=√(3)`

`√(3)=(12)/(y)`

`y=(12)/(√(3))`

Simplify

`y=12(√(3))/(3)`

`y=4√(3)\ units`

In the right triangle of the left side

`sin(60\°)=(12)/(z)`

`sin(60\°)=√(3)/2`

`√(3)/2=(12)/(z)`

`z=(24)/(√(3))`

Simplify

`z=24(√(3))/(3)`

`z=8√(3)\ units`