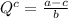Answer:
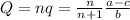
if n=1 (monopoly) we have
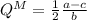
if n goes to infinity (approaching competitive level), we get the competition quantity that would be
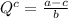
Step-by-step explanation:
In the case of a homogeneous-good Cournot model we have that firm i will solve the following profit maximizing problem
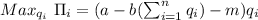
from the FPC we have that
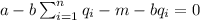
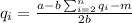
since all firms are homogeneous this means that
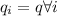
then
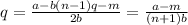
the industry output is then
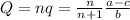
if n=1 (monopoly) we have
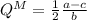
if n goes to infinity (approaching competitive level), we get the competition quantity that would be