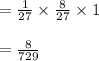Answer:
Number of Questions =3
Probability of giving a correct answer
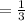
Probability of giving two correct answers
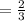
Probability of giving all correct answers
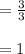
Probability that at least one of them is correct
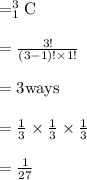
Probability that two of them is correct
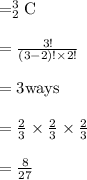
Probability that all of them is correct
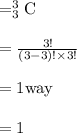
So, Required probability